一年的教学生涯即将过去，可以说紧张忙碌⽽收获良多。作为一名刚进入教育行业不久的新教师，我在认真执行学校教育教学工作计划的同时，也在思考一些关于数学学科本身的问题，数学是一门非常严谨抽象的学科，我们教师在教育教学中，往往比较注重教学逻辑和解题的思想方法，而忽略了知识本源，从而导致课堂气氛压抑，学生乏味无趣，教学效果收效甚微，但要切实上好一节数学课，让学⽣听得有趣、学得轻松是一件比较困难的事情。学生也会产生我们为什么要学习数学这门抽象课程的疑问，这些数学公式或者思想是怎么来的？有没有文化可循？教师设计好课堂的情景导入是非常重要的，如果课堂的开始就能激发学⽣的求知欲，使整个课堂⾮常的活跃，也许能达到事半功倍的课堂教学效果。那么怎样才能达到这样的效果呢？我想让数学文化融入高中数学课堂是个不错的选择，让学生了解数学文化，了解数学知识的产生发展，数学作为物理学、天文学等自然学科的基础，它所体现出来的价值有多大。数学语言、数学曲线、数学符号等其中所蕴含的美学是多么奇妙，数学也是有文化承载的，而不仅仅是枯燥的公式与算法。

历史的发生原理告诉我们，学生对数学概念的理解过程与数学概念的历史发展过程具有一定的相似性，历史上的数学家所遭遇的困难正是学生会遇到的障碍。

因此，借鉴数学概念在历史上的发生和发展过程来讲授该概念，往往更符合学生的认知规律，有助于他们把握教学难点。新课改后，数学课程内容突出了函数、几何与代数、统计与概率等模块，强调数学建模数学探究，注重数学文化贯彻始终。十八大明确提出把“立德树人”作为教育的根本任务，全面实现素质教育，那么数学这门学科在教学中如何实现德育？如何在教学中培养学生的核心素养？这也是我们数学老师需要深入思考的问题。下面我就数学文化在高考、德育、美育、人文科技领域以及多元文化融合等几个方面的渗透谈一些想法。

1 基于数学文化的高考题

 这道题选自2017年浙江高考卷第11题，背景是魏晋时期的数学家刘徽首创的割圆术，所谓割圆术即通过圆内接正多边形细割圆，并使正多边形的周长无限接近圆的周长，进而求得较为精确的圆周率，其基本思想是极限与无穷小分割。刘徽把圆内接正多边形的周长一直算到了正3072边形，并由此而求得了圆周率为3.1415和3.1416这两个近似数值。这个结果是当时世界上圆周率计算的最精确的数据，后面祖冲之在刘徽的基础上继续努力，终于使圆周率精确到了小数点以后的第七位。在西方，这个成绩是由法国数学家韦达于1593年取得,比祖冲之要晚了一千一百多年。本题以此为试题背景，不仅让学生感叹祖先的智慧，也能增强学生的自豪感，培养学生的创新意识。

下图来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC和直角边AB，AC。ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ。在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别为p1,p2,p3。则

A p1=p2    B p1=p3   C p2=p3   D p1=p2+p3

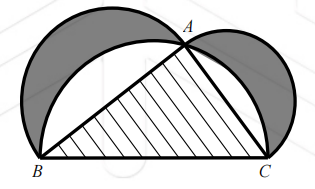
这道高考题选自2018年全国一卷，这是古希腊数学家希波克拉底发现的平面几何的优美定理：以直角三角形的两个直角边向外作两个半圆，以斜边向内作半圆，则三个半圆所围成的两个月牙图形的面积之和等于该直角三角形的面积。数学学科蕴含丰富的审美因素，具有很高的美学价值，其表现形式是对称美、简洁美、奇异美与和谐之美，在高考中也是经常体现。

纵观这些年的高考数学，渗透数学文化的试题不仅将数学知识、数学思想方法、数学精神融为一体，充分体现了高考命题注重体现数学的科学价值和人文价值的理念，渗透数学思想方法的同时不仅发挥高考育人功能与和导向作用，也积极培养与践行社会主义核心价值观。

2 数学文化在课堂中的德育功能

由《塔木德经》产生的数列问题：任何一个看望病人的人能消除其疾病的六十分之一，问题是第60个人看望该病人后，其病情如何？

第1，第2，第3，........第n个人看完病人以后，病情构成等比数列这个事例取自《塔木德经》，可以作为等比数列概念的情景引入。《塔木德经》是犹太人生活中除《希伯来圣经》以外最重要的典籍，它在多数时候也被人叫做犹太教法典。经书中有很多发人深思的小故事和语录，它不仅教会人们思考什么，还教会他们如何思考。本事例中，在知识层面看到当公比为小于1的正数时，等比数列具有递减的性质，也从人文角度提倡多关怀多鼓励，当他人处于逆境时给予温暖，让学生懂得付出与感恩，体现数学的德育功能。

3 数学文化在课堂中的美育以及在人文科技领域的辅助作用

有些学生学过解析几何后，不知道为什么椭圆、双曲线和抛物线统称为圆锥曲线，双曲线与椭圆到底是亲如一家还是形同陌路？

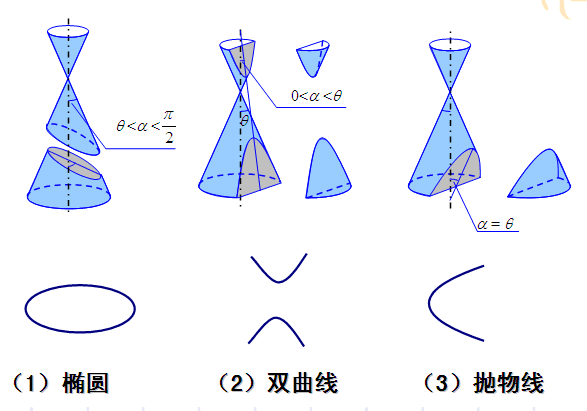 2000多年前，古希腊数学家阿波罗尼斯采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥，得到的是圆；把平面渐渐倾斜，得到椭圆；当平面倾斜到“和且仅和”圆锥的一条母线平行时，得到抛物线；用平行于圆锥的轴的平面截取，可得到双曲线的一支，把圆锥面换成相应的二次锥面时,则可得到双曲线，所以圆锥曲线是由圆锥界面而统一定义的。这其中的玄妙是不是很美？笛卡尔认为“美是一种恰到好处的协调和适中”。三种曲线正是从某些层面揭示了客观世界的和谐统一。圆锥曲线优美对称，是人类智慧的体现也是大自然深层结构美的折射。生活中小到瓶瓶罐罐，大至很多建筑的造型都是从圆锥曲线的线条美中得到灵感。圆锥曲线几种表达式也存在着内在和谐，所以圆锥曲线是内在美与形式美的统一。

除此之外，圆锥曲线在科技领域的价值更大，我们生活的地球每时每刻都在环绕太阳的椭圆轨迹上运行，太阳系其他行星也如此，太阳则位于椭圆的一个焦点上。如果这些行星运行速度增大到某种程度，它们就会沿抛物线或双曲线运行。人类发射人造地球卫星或人造行星就要遵照这个原理。相对于一个物体，按万有引力定律受它吸引的另一物体的运动，不可能有任何其他的轨道，因而圆锥曲线在这种意义上讲，它构成了我们宇宙的基本形式。另外它的光学性质，了解古生物学中某些化石的圆锥截面可以帮助了解某些生物体的三维形状等，这些方面的作用让它的价值无与伦比。

4 课堂中多元数学文化融合

很多老师在讲解等差数列求和公式时会引用德国数学家高斯小时候的典故，在高斯读小学的时候老师出了一道题，从1连续加到10，当别的同学还在奋笔疾书时高斯已经把答案算出来了，高斯采用的是倒序相加法，1+100,2+99,3+98，......每一对的和都是101，一共有50对，结果就是5050.其实我国数学家杨辉早在700多年前就提出了这样倒序相加的思想，而且比高斯早了500年。

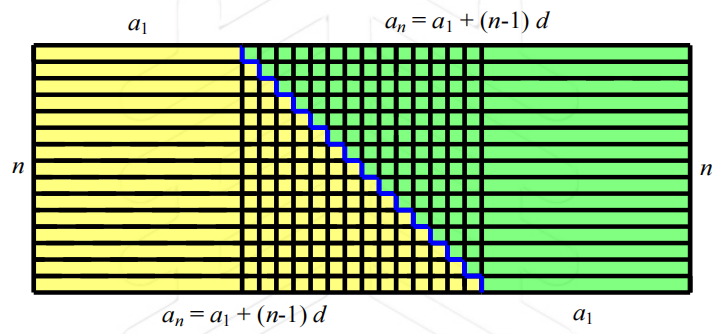
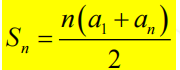
   不同文化背景下的同一种数学思想，在课堂上碰撞多么美妙。学生在感叹高斯是数学天才的同时也会对我国数学家肃然起敬，杨辉是我国南宋杰出的数学家，他在总结民间乘除捷算法、“垛积术”、纵横图以及数学教育方面，均做出了重大的贡献。

数学之为学，有其独特之处。它本身是寻求自然界真相的一门科学，数学家研究大自然所提供的一切素材，寻找它们共同的规律，并用数学的方法表达出来。数学展现出来的大自然的真和美，远远胜过一切人为的造作。我想在平时的教育教学中，教师应时刻树立数学文化的意识，不仅让学生感叹数学家们惊人的智慧以及现实世界中数学规律的奥妙与神奇，还要让学生受到数学文化的熏陶，提高学生的数学素养。