一、教材分析

1. 知识点清单：平面向量数量积的几何意义，平面向量数量积的运算法则与影响因素，投影向量与平面向量数量积的运算律，平面向量数量积的数形结合

2. 本章的意义及作用：承上启下，平面向量的概念、加减法以及数乘更多强调的是平面向量的几何性质，而数量积则是平面向量从几何性质走向代数意义的过渡环节

二、学情分析

1. 学生特点：学生在前几节课通过物理模型已经感悟了平面向量加减法以及数乘的运算法则及其合理性，因此自然而然地会猜想和思考平面向量之间是否可以“相乘”，从物理模型出发，可以减小学生的认知阻碍，并激发学生的探究兴趣

2. 矛盾冲突：新运算法则与旧运算法则的冲突、向量的代数意义和几何性质之间的冲突

三、教学设计

1. 情境导入：通过物理学中的“矢量相乘”模型（拉力做功模型）类比得出平面向量数量积的运算法则，期间需要强调三个细节问题：①平面向量数量积的结果一定是数量而不是向量②平面向量数量积之间的运算符号必须是“点乘”③影响平面向量数量积的因素除了两个向量的模以外还有两个向量夹角的大小

2. 公式巩固：通过两道例题（根据向量的模和夹角求数量积，根据向量数量积和模反求夹角）引导学生感悟公式的正用和逆用，期间可以让学生体会到影响数量积正负的是两个向量夹角的余弦值，在此基础上，通过三道概念辨析题帮助学生理解和感悟“夹角为锐角是数量积为正数的充分不必要条件”这一常考易错点

3. 概念深入：通过物理学中分力做功的等价性，引导学生感悟投影向量的运算公式及其合理性，此部分要求学生了解即可，不应花费过多的时间，再由投影向量的概念引出本节课的重难点：平面向量数量积的运算律（不满足消去律和结合律）

4. 综合探究：在学生已经熟悉平面向量数量积的基本概念、平面向量数量积的运算法则、平面向量数量积的运算律这些新知的基础上，通过以下几道例题引导学生感悟平面向量数量积的代数意义，通过数量积，我们可以利用代数运算的方式来发掘向量的几何性质，并通过向量来研究平面几何，从而使学生深刻感悟到向量的意义与价值

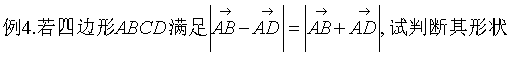
四、课后作业

采取分层作业的方式，选做题与必做题相结合，满足不同层次学生的求知需要

书上例题以及《全优学练测》上的关键能力提升部分