8.2.2　离散型随机变量的数字特征

知识点　离散型随机变量的均值

一般地，随机变量X的概率分布如表所示，

其中p_i≥0，i＝1，2，…，n，p₁＋p₂＋…＋p_n＝1.我们将E(X)＝μ＝p₁x₁＋p₂x₂＋…＋p_nx_n称为随机变量X的均值或数学期望．

点一点：

对离散型随机变量的均值的再理解

(1)离散型随机变量的均值是刻画离散型随机变量取值的平均水平的指标；

(2)由定义可知离散型随机变量的均值与它本身有相同的单位；

(3)均值是一个常数，在大量试验下，它总是稳定的，不具有随机性．　　

想一想：

若随机变量X服从两点分布且P(X＝1)＝P，则X的均值是多少？

提示：E(X)＝1×P＋0×(1－P)＝P.

 [例1]　猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名．某嘉宾参加猜歌名节目，猜对每首歌曲的歌名相互独立，猜对三首歌曲A，B，C歌名的概率及猜对时获得相应的公益基金如表所示.

规则如下：按照A，B，C的顺序猜，只有猜对当前歌曲的歌名才有资格猜下一首．求嘉宾获得的公益基金总额X的分布列及均值．

小结：求离散型随机变量均值的一般步骤

第一步是“判断取值”，即判断随机变量的所有可能取值；

第二步是“探求概率”，即求出随机变量取每个值时的概率；

第三步是“写分布列”，即按规范形式写出分布列，并注意用分布列的性质检验所求的分布列或某事件的概率是否正确；

第四步是“求均值”，利用均值的定义求均值．　　　　

[跟踪训练]

某地举办知识竞赛，组委会为每位选手都备有10道不同的题目，其中有6道艺术类题目，2道文学类题目，2道体育类题目，每位选手从给定的10道题中不放回地随机抽取3次，每次抽取一道题，回答完一道题后，再抽取下一道题进行回答．

(1)求某选手在3次抽取中，只有第一次抽到的是艺术类题目的概率；

(2)求某选手抽到体育类题目的次数X的均值．

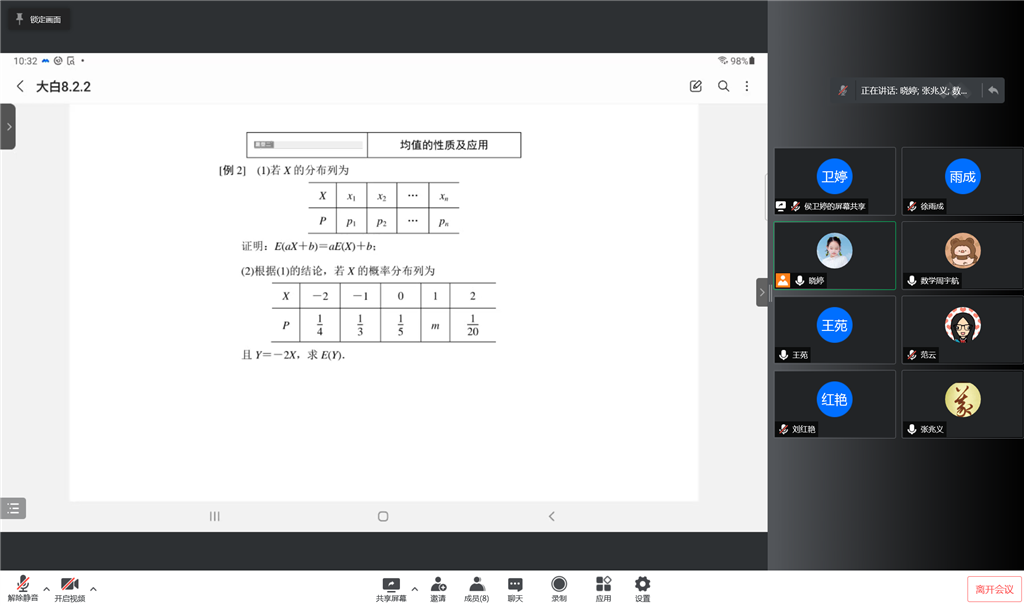
[例2]　(1)若X的分布列为

证明：E(aX＋b)＝aE(X)＋b；

(2)根据(1)的结论，若X的概率分布列为

且Y＝－2X，求E(Y)．

 [母题探究]

(变设问)若本例(2)条件不变，若ξ＝aX＋3，且E(ξ)＝－，求a的值．

解：E(ξ)＝E(aX＋3)＝aE(X)＋3＝－a＋3＝－，解得a＝15.

小结：与离散型随机变量性质有关问题的解题思路

若给出的随机变量ξ与X的关系为ξ＝aX＋b，a，b为常数．一般思路是先求出E(X)，再利用公式E(aX＋b)＝aE(X)＋b求E(ξ)．也可以利用X的分布列得到ξ的分布列，关键是由X的取值计算ξ的取值，对应的概率相等，再由定义法求得E(ξ)．　

反思：教材从一个具体的例子入手，引入离散型随机变量的概念。教学中要充分的分析一些实际问题，在活动中比较离散型随机变量的均值和以前学习过的样本平均数之间的异同。

在例题讲解过程中，及时和学生一起总结方法，帮助学生加深对所学知识的理解和掌握。