适用

年级

高二年级

总课时

16

课程

类型

物理思维类

课程简介（200字内）

著名的物理学家费曼曾对数学与物理的关系进行了系统的阐述，被称为“最伟大的讲解员”，讲话中提及物理学不是数学，数学也不是物理学。但它们能够相互帮助。

我们常听到“数理化不分家”，我们常听说“数学学不好的人物理也不会太好”，的确，数学方法在物理学科中的应用随处可见，

本课程既不是单纯的物理学，也不是单纯的数学，本课程旨在挖掘物理学科中的数学思想以及数学思想在物理学科中的应用。

背景

分析

（500字内）

一方面，学习数学能够提升学生的逻辑思维，锻炼学生的逻辑推理能力，使得学生自身的能力得以提升。另一方面，当物理达到一定难度时，我们需要数学知识来帮助解决物理问题，就像大学生大一的时候就要学习一门《高等数学》，到了大三就要学习一门《数学物理方法》一样。

再从更大层面阐述，很多物理发现都是由精密的数学知识推演而来，例如开普勒三大定律都不是直接来自于数据，而是经过复杂的推导演算加猜想得到的。以第一定律（椭圆定律）为例，在所有行星的椭圆轨迹中，即便是形状最扁的水星，其短轴也只比长轴短2%，而且由于距离太阳太近，会随着日落、日升而消失，并不便于观测。而被开普勒用来确定第一定律的火星，其轨迹的短轴只比长轴短0.5%，即便是被当作正圆形，其预测误差也在当时观测精度所允许范围内，并不容易引人怀疑。所以我认为这便是不尊重数学的后果。其次，数学也能够验证假说，开普勒三定律自出世以来，并不是毫无无争议，大家的抱怨主要集中在面积定律上，因为当时没有微积分，面积定律难以用于直接计算行星位置，后来形成的数学微积分才让开普勒从竞争者中脱颖而出。

综上所述，不管是当下还是着眼于更高层次的发展，数学思想在物理学科中的应用都是值得我们认真挖掘的。

课程

目标

1.知道在物理学科中，有哪些常见、重要的数学知识。

2.掌握运用数学知识解决物理问题的方法。

3.提升学生的数学物理思维品质。

4.体会数学思想在物理学科中的重要性。

学习主题/活动安排（请列出教学进度，包括日期、周次、内容、实施要求）

本课程分为五个单元：

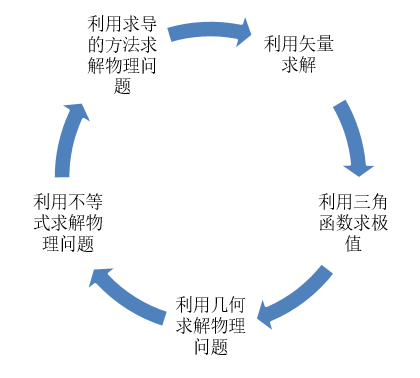
首先，在物理题里面，我们需要通过所学物理规律把题目中的已知量和未知量组织在一起，通常情况下，我们会列很多式子。如果想要迅速要解出这些未知量，解方程的能力就必须足够的强。所以，要学好高中物理，就必须学会解方程。

再者，在做物理题时经常会涉及到解图形问题，这就要求学生的数学中的几何学的必须足够好。就比如说光学里面的作图问题，带电离子在磁场运动中，半径的确定问题，还有我们常见的力的合成与分解问题，这些都涉及到数学里面的几何问题。

运用数学知识来解决物理问题的一般有哪些？这里简单概括一下：

课时1：分享课程纲要 厘清教学目标

单元一：利用几何求解物理问题

课时2：力的合成与分解

课时3：几何光学

课时4：带电粒子在磁场中运动

课时5：带电粒子在组合场中运动

课时6：带电粒子在叠加场中运动

通过分析物理过程遵循的物理规律，找到变量之间的函数关系，做出其图像，由图像可求得答案。

单元二：利用不等式求解物理问题

课时7：力学中临界速度、临界力的求解

课时8：电磁学中临界电场强度、磁感应强度的求解

课时9：选修模块中核能计算

单元三：利用求导的方法求解物理问题

课时10：位移、速度与加速度

课时11：求导的链式法则在位移与速度图像中的应用

单元四：利用三角函数求极值

课时12：曲线运动中的三角函数关系，如平抛运动

课时13：磁场中的三角函数关系

单元五：利用矢量求解

课时14：力与运动

课时15：曲线运动中的速度变化量

课时16：动量守恒定理中的矢量关系

物理是科学,而数学是研究经典物理的工具.。所以有句俗话,物理学家同时一定也是数学家,牛顿不仅发现了万有引力,顺便还能求导搞微积分。在平时学习中应注意以下两点：

一是在学习物理的过程中，要多联系生活实际，要常联系自然现象。二是在学习物理的过程中，要学会善于应用数学知识来帮助学习物理。这样可以使数学、物理同时进步。

评价活动/成绩评定

l    本课程最后成绩以A、B、C、D四个等级公示并记录。

l    评价依据：平时作业+最终考核+模型制作。各部分评价要点如下：

1.平时作业：能够按照规范式利用数学知识解决物理问题，计算出正确答案，占比30%。

2.最终考核：满分100分，折算成60分计入总分，占比60%。

3.模型制作：制作磁场旋转圆模型，占比10%。

l    评价者：平时作业与最终考核：教师评价、模型制作：同学互评。

互评表（A、B、C、D等级）

l    成绩来源：A等级：80分及以上、B等级：70~80分、C等级：60~70分、D等级：60分以下。

主要参考文献

[1]王凡,邵云,窦瑾.谈谈数学知识在物理解题中的应用[J].湖南中学物理,2020,35(02):85-88.

[2]骆新民.如何提高高考物理中应用数学知识解决物理问题的能力[J].课程教育研究,2019(32):6.

[3]谢晓敏.数学思想方法在物理问题解决中的应用[J].中学物理教学参考,2019,48(10):6-7.

[4]张爱英.论数学建模在物理中的应用[J].中学物理教学参考,2018,47(20):12-13.

备 注