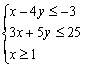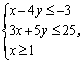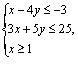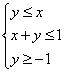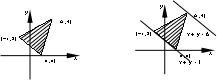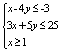教学环节

教学内容

师生活动

设计意图

一、

复

习

回

顾

复习回顾，引入本节课要研究的数学问题

（1）引导学生在同一直角坐标系下作出下列直线，并找出它们之间的关系：

师生共同回顾前面所学内容，在作出5条直线的图像的基础上，分析出它们之间的关系结论：

①形如

②k<0时，k越大，直线的倾斜角

唤起学生对直线位置关系的回忆，为本节课利用数形结合的方法解决线性规划问题打下础。

二、

创

设

问题，引

入

新

课

（2）引导学生作出下列不等式组所表示的平面区域

问题①

问题②

问题③

首先由学生回答前两个问题，在小组讨论后请一位学生代表回答第三个问题，并说出他的理由。然后教师提问“我们能不能用

让学生产生进一步学习的欲望，即如何能解决这种最值问题。

用学生已有的知识结构不能解决，从而使学生产生学习新知识的愿望．

师生共同解决问题③，将问题③以例题形式出现

（3）已知

 （1）引导学生”以

（2）师生共同确定想法：

利用数形结合的思想解决问题.

让学生自主探究，体验数学知识的发生、发展的过程，体验转化和数形结合的思想方法。

三，学生自主合作探究

（4）由学生自己按照分好的学习小组，合作交流，自主探究．

教师在巡视中，努力做到：

（1）引导学生利用

（2）教师根据课堂情况，合理引导小组的探究法方向，体会数形结合的思想．

（1）让学生在画图的过程中感受数形结合的思想.

（2）理解

（5）教师组织学生以小组为单位进行探究成果展示

（2）教师借助图象进行动态演示，同时归纳出本题的解题步骤：

①作出不等式组

通过数与形的结合，

四，引

入

概

念

（6）在理解本题的基础上，向学生介绍线性规划的相关概念

解释最优解，同时交代求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。

通过对例题的分析， 加深学生对线性规划问题相关概念的理解.

五，课

堂

练

习

（7） 课堂练习

练习.求

（1）从学生的已有知识出发，让学生独立完成两道练习题，上台板演，让学生感受利用数形结合思想解决线性规划问题的一般过程；

（2）重点强调解决本题的关键是对

(3)规范解决线性规划问题的一般步骤．

在给出引例和线性规划的定义后，及时通过练习帮助学生整理答题思路，再次强化图解法的基本步骤和规范解答的表述过程，同时加深对相关概念的理解。

对线性规划问题的再认识

例2．已知

①

② 请你设计一个目标函数，使得其最大值点在B处取得？

③ 请你设计一个目标函数，使得其取最优解的情况有无穷多个？

引导学生在探究的环境下，自己发现、归纳线性规划问题中目标函数的最值与平行直线族在

创设一个探究、讨论的课堂氛围，激发学生的学习情趣，增强师生、生生之间的互动，体现新课程中让学生“做中学”的理念；

六，课堂小结，凝练提升

（9）课堂小结，凝练提升

为使学生对所学的知识有一个完整而深刻的印象，我引导学生从以下两方面自己小结。

（1）这节课学习了哪些知识？

（2）学到了哪些思考问题的方法？

(1)学生自主思考后，课堂集中交流，师生互相补充完善．

(2)教师适时点拨和引导，小结应包含如下方面内容：

一、知识方面：相性规划问题的相关概念； 解决线性规划问题的步骤；

二、数学思想方法：数形结合的数学思想

让学生通过小结，反思学习过程，加深对线性规划问题的认识，领会研究问题的方法，明确研究问题的步骤，体会其中蕴含着的数形结合的思想. 

六，布置作业

（10）布置作业

1.完成课本P93 第4题

且变量x、y为整数,求z的最大值和最小值。

（1）通过作业发现和弥补教学中的不足，注重个体差异，因材施教；