极化怛等式

变（1）：

变（2）：

如图，在△ABC中，边BC的四等分点依次为D，E，F．若→(AB)·→(AC)＝2，→(AD)·→(AF)＝5，则AE的长为       ．

变（3）：

如图，在

中，点M为边BC的中点，且AM=2，点N为线段AM的中点，若

,则

      ．

变（4）：

如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点

，

，则

的值是   ▲    .                                        

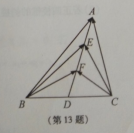
变（5）

如图，△ABC为等腰三角形，

，

，以A为圆心，1为半径的圆分别交AB，AC与点E，F，点P是劣弧

上的一点，则

的取值范围是   ▲   ．

思考：

        

反思;

  自向量引入高中数学以后，由于它独特的性质(代数与几何的桥梁)，在近几年全国各地的高考中迅速成为创新题命制的出发点，向量试题有着越来越综合，越来越灵活的趋势，在江苏省数学高考中尤为突出，也出现了一些非常精美的向量题。

(1)极化恒等式源于教材又高于教材，书上有2个重要的向量三角关系，而极化恒等式无非就是这2个公式的逆用;

(2)具有三角儿何背景的数学问题利用极化恒等式考虑尤为简单，让“秒杀向量”成为另一种可能;

(3)向量是连接代数与几何的桥梁，由于向量的坐标运算引入，向量与代数的互换运算可以说是深入人心，而与几何的运算联系略显单薄，而极化恒等式恰恰弥补了这个缺憾，可以说极化恒等式应该是把向量的数量积问题用形象的几何图形展示得淋漓尽致。

an>