数列求和复习

教学目标：1、掌握数列求和常用的方法（公式法、倒序相加法、错位相减法、分组求和法、并项求和法、裂项相消法）；

2、能应用数列求和解决一些数列问题，体会解题过程中蕴含的函数思想以及分类讨论思想。

重点：非等差、等比数列的求和方法（错位相减法、裂项相消法、分组求和法、并项求和法）

难点：数列中函数思想的应用

教学方法：启发式教学法，问题引导，投影仪等现代教学手段辅助教学，充分发挥学生的主观能动性

教学设计：

一、预习作业

1、正项数列

满足：

（1）求数列

的通项公式；

（2）令

求数列

的前

项和

.

2、求数列

的前

项和

.

3、设数列

的前

项和为

，数列

是各项均为正数的等比数列，且

.

（1）求数列

，

的通项公式；

（2）设

，求数列

的前

项和

；

（3）设

，求数列

的前

项和

二、复习引入

数列求和主要分为两类，一类是我们熟悉的等差、等比数列的求和，我们一起把公式回忆一下：

等差数列：

等比数列：

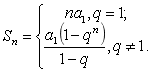
另一类是特殊数列（非等差、等比数列）的求和，我们常见的方法有哪些呢？学生一起回答.（倒序相加法、错位相减法、分组求和法、并项求和法、裂项相消法）

下面我们主要针对预习作业上的几个题目，对裂项相消法、错位相减法、分组求和法、并项求和法做一个系统地总结深化。

三、探究深化

例1 正项数列

满足：

（1）求数列

的通项公式；

（2）令

求数列

的前

项和

.

分析：这道题目给出的是关于

的一元二次方程，学生很容易解决第一小问，但在具体过程中不要忽视条件

；第二小问考察的是裂项相消法，题中数列

通项公式为

一些学生对裂项相消法本质不了解，为此犯了这样的错误：它把数列

通项公式写成

然后

对于这样的问题可以利用投影展示并分析指正。

变式1：对例1中得到的

，若

对任意

恒成立，求实数

的范围。

分析：这一问主要考察的是恒成立问题，学生容易上手，但如何求

的最小值，部分学生可能有难度。在教学中充分引导学生把

与已学过的初等函数模型结合，从而借助单调性来得到

的最小值。在这个地方，可以进一步这样提问：你能给出

的一个简单的范围估计吗？

例2 求数列

的前

项和

.

分析：在这个问题上，学生容易犯的错误在两个地方：1.求和不知道关注数列通项，这是对求和本质的一个不理解。如果这道题目直接给出通项公式

，会求和的学生人数会大大增加；2.在求和过程中，部分学生容易在最后通分这一步出现小问题。

可以让学生进一步思考：如何求数列

的前

项和？这样就完整的复习了裂项相消法的三种类型。同时，在教学中，应突出求和关注通项这一重点。

例3设数列

的前

项和为

，数列

是各项均为正数的等比数列，且

.

（1）求数列

，

的通项公式；

（2）设

，求数列

的前

项和

；

（3）设

，求数列

的前

项和

分析：第一问考察的是已知

求

的方法以及数列中基本量的运算，难度不大，已知

求

的时候不要忘了分

；第二问是错位相减法的考察，学生使用错位相减法的前提以及基本步骤都没问题，主要还是计算的细节，在教学中，可以借助投影仪展示学生错位相减法的问题所在之处，这样效果比较法；第三问考察的是分组求和法以及并项求和法，主要的难点存在于并项求和法，学生对这种方法的使用不够熟练。

在上课过程中，可以设置如下的变式：

对于例3（1）：

变式3.1 求数列

的前

项和

.

对于例3（2）：

变式3.2 若

 对

恒成立，求

的范围.

这个题目的设置，是对前面例1变式的一个深化和补充，让学生掌握如果无法借助已学函数模型直接得到单调性，那么我们可以利用作差作商的方法，这也是一个难点。

对于例3（3）：

变式3.3 求数列

的前

项和

.

这个变式的设置，是对第（3）问的一个深化，需要借助奇偶性来讨论，对学生分类讨论的能力以及数学思维有一定的要求。

四、课堂小结

1、常用求和方法：

裂项相消法、错位相减法、分组求和法、并项求和法

2、数列中函数思想的应用

数列求和复习教学反思

本节课主要是复习非等差、等比数列的几种常用求和方法，具体包括裂项相消法、错位相减法、分组求和法以及并项求和法，在复习过程中，注意函数思想以及分类讨论数学思想方法的渗透。在课前，我布置了三道对应的数列求和题目，并通过批改知道了学生存在的一些问题，在课堂上借助投影仪展示点评学生的一些做法，获得了不错的效果。

在具体的课堂教学中，我还存在着一些不足。

第一，对于例1中的变式：若

对任意

恒成立，求实数

的范围。学生上手容易，但具体如何求

的最小值缺乏思路，甚至有学生站起来回答利用基本不等式。而我在教学前还认为这类题应该很多学生会有想法，会想到利用单调性。这样一个错误的预判导致我在教学中没有在这里给出充分的引导和思考时间，虽然我后来也加以了强调，但没有达到理想的效果。

第二，对于例3（2）：设

，求数列

的前

项和

.在讲解过程中，我投影了部分学生的答案，也让学生互相之间看到了彼此的错误之处，并请学生做了一定的点评。但其实在课后作业的练习上发现错位相减法还是有很多的问题，可见课上虽然给出了方法步骤，指出了一些已有的错误，但缺乏课堂及时地实战训练，一些细节就会流于形式，再加上学生有一些不好的学习习惯，细节容易出错，所以我感觉这一块课上应该花更多地时间，这样才会看出效果。

第三，由于时间安排上的不合理，例3（3）的讲解有些匆忙，其实这个问题也是本节课的一个难点。例3（3）：设

，求数列

的前

项和

.从课前预习作业反馈的情况也可以看出学生对于并项求和法掌握得不理想，甚至可以说很多同学没有这个并项的意识。但我在这一块讲解地不够细致，还很匆忙的给出了一个变式，让学生直接求解

，虽然也有一些学生会，但很多学生的课堂反应让我看到了一丝迷茫。所以我感觉在这个地方我不应该赶，而是应该稳扎稳打，先把基础的

讲懂，让学生对并项求和什么时候用、怎么用、好处是什么有深入的了解。而这个变式可以放在课后，作为一个思考题，对于学生提高自己的思维能力有帮助。

    通过本节课的教学，我也深刻意识到：我们的教学是时时刻刻、紧紧围绕学生的，一定要从学生实际出发，在重难点要舍得花时间，要让尽可能多的学生真真正正地学懂学透。

an>