课题：解析几何中的定值问题

【教学目标】学会合理选择参数（坐标、斜率等）表示动态图形中的几何对象，探究、证明其不变性质，体会“设而不求”、“整体代换”在简化运算中的作用． 反思解法的自然性;多样性;简洁性 ;可操作性;疏漏之处

【教学难、重点】解题思路的优化．

一、知识梳理：

掌握处理解析几何中常见的定值问题处理方法.

二、典型例题：

    解析几何中的定值、定点、定线问题仍是高考考试的重点与难点，都是探求"变中有不变的量".一般运用函数与方程、转化与化归、数

形结合、分类讨论、特殊到一般、相关点法、设而不求、换元、消元等基本思想方法.

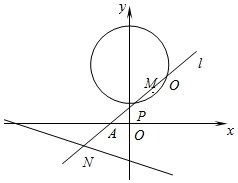
1、已知过点

相交于P，Q两点，M是PQ的中点，l与直线

相交于点N．

(1) 求证：当l与

垂直时，l必过圆心

；

(2) 

探索

是否与直线l的倾斜角有关,若无关,请求出其值,若有关,请说明理由．

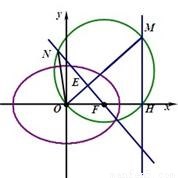
2、已知椭圆的中心为坐标原点，短轴长为2，一条准线方程为

．

（1）求椭圆的标准方程；

（2）设

为坐标原点，

是椭圆的右焦点，点

是直线

上的动点，过点

作

的垂线与以

为直径的圆交于点

,求证:线段

的长为定值．

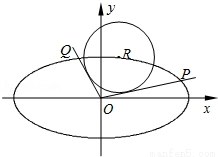
3、如图，在平面直角坐标系

中，已知椭圆

，设

是椭圆

上的任一点，从原点

向圆

作两条切线，分别交椭圆

于

两点．

（1）若直线

互相垂直，求圆

的方程；

（2）若直线

的斜率存在，并分别记为

，求证：

；

（3）试问

是否为定值？若是，求出该值；若不是，请说明理由．

 

教学反思:

    数学教学离不开解题教学.我们经常有这样的感受,在讲解题目时会出现讲了但讲得不到位, 学生理解不是很透彻,讲了但选择的方法不够好,学生不易掌握.究其原因,或是由于时间仓促,准备不充分造成的;或是由于自身水平有限,认识肤浅造成的;或是由于对学情估计不足,把握不到位造成的,总之,数学解题教学环节中有时不可避免地存在着一些问题，暴露出一些不足,也给教师自己留下了一些遗憾.

解题教学之后, 总有不少感想和收获.其中可能存在一些遗憾.比如所授解法比较繁琐,不自然或是技巧性强,学生不易掌握.抓住这些不尽如人意的点,给自己提一些问题:

(1) 有没有更贴近学生思维实际的解法──反思解法的自然性;

(2) 有没有其他好的解法──反思解法的多样性;

(3) 有没有更简单的做法──反思解法的简洁性 ;

(4) 是不是学生易接受的方法──反思解法的可操作性;

(5) 是不是少考虑特殊情况──反思解法的疏漏之处;

有学生提出这样的问题,老师我当时直接从代数角度想的:

     以OM为直径的圆方程

,直线

联立

              

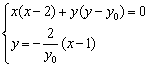
想解出

的坐标,可是解不出来,我这样能做下去吗?

之前我翻阅过学生的试卷,他的这种做法具有普遍性,不少同学是这样做的,最后因难而废.

像这样抛一些问题,从不同的角度进行反思,可以发现一些不足.尝试改进之后,会得到很多有价值的东西.教学遗憾及对其反思可以提升数学教师的数学教学机智与智慧，使教师向自己（的数学教学）学习,才可能避免更多的遗憾.教师通过主动的,有意识地对已经发生的教育过程的回头再思考，从中不仅可以评估实践活动的效果和成败，发现不足之处, 还可以为下一阶段的教学积累备课素材.

empInsertTag">