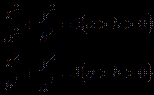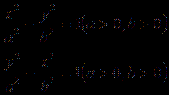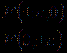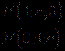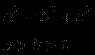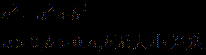《双曲线的标准方程》

一、教学目标
1.理解双曲线的定义并能独立推导标准方程;
2.通过定义及标准方程的挖掘与探究,使学生进一步体验类比、数形结合思想方法的运用,提高学生的观察与探究能力;
3.通过教师指导下的学生交流探究活动,让学生体会数学的理性和严谨,培养学生实事求是和锲而不舍的钻研的精神,形成学习数学知识的积极态度.
二、教学重难点
重点:理解和掌握双曲线的定义及其标准方程.
难点:双曲线标准方程的推导.
三、教学过程
(一)创设情境
1.生活中的双曲线:PPT展示.
2.双曲线的定义
平面内到两定点
![]()
![]()
![]()
![]()
![]()
![]()
几何画板演示
(二)数学建构
1.复习回顾
问题1: 求椭圆标准方程的步骤是什么?
(1) 建系 (2)设点 (3) 列式 (4)代入 (5) 化简(检验)
问题2: 如何化简:
![]()
移项平方:
![]()
整理得:
![]()
问题3:如何处理
![]()
设
![]()
![]()
2.思考
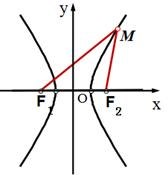
问题1: 如何求双曲线的标准方程?
(1)
![]()
![]()
![]()
![]()
(2)设点 设
![]()
![]()
![]()
![]()
(3)列式
![]()
(4)代入
![]()
(5)化简
法1:等式两边同时平方得:
![]()
![]()
整理得:
![]()
![]()
等式两边同时平方得:
![]()
处理1:
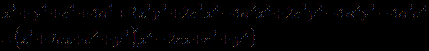
处理2:
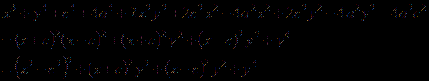
![]()
![]()
整理得:
![]()
![]()
法2:去掉绝对值得:
![]()
移项两边平方得:
![]()
![]()
整理得:
![]()
两边再平方后整理得
![]()
问题5: 如何处理
![]()
由双曲线定义知:
![]()
![]()
![]()
![]()
![]()
问题2:试比较这两种化简方法,你有什么收获?
3.双曲线的标准方程
焦点在
![]()
![]()
![]()
焦点在
![]()
![]()
![]()
问题:如何判断焦点在哪个轴上?
练一练: 判断下列各双曲线方程焦点所在的坐标轴并求出a,b,c各为多少?
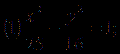
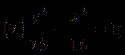
![]()
![]()
(四)课堂小结
双曲线与椭圆之间的区别与联系
|
椭圆 |
双曲线 |
|
|
定义 |
|
|
|
方程 |
|
|
|
焦点 |
|
|
|
a,b,c的关系 |
|
|
(五)课后作业
1. 平面内两个定点的距离等于10,一个动点M到这两个定点的差的绝对值等于8.建立适当的坐标系,求出动点M的轨迹方程.
2.求适合下列条件的双曲线的标准方程:
(1)已知
![]()
![]()
![]()
(2)一个焦点为
![]()
![]()
(3)经过点
![]()
《双曲线的标准方程》的教学反思
本节课首先通过创设情境:生活中的双曲线的PPT的展示给学生形象的感受进而引出双曲线的严格定义,通过双曲线的几何画板演示加深学生对双曲线的定义理解。
前面从形的角度去认识双曲线接下来从数的角度去认识双曲线即去研究双曲线的标准方程。研究双曲线的标准方程之前让学生回顾求椭圆标准方程的步骤,这样学生可以通过类比的思想去处理双曲线的标准方程。
在双曲线标准方程的推导过程中要化简
![]()
这一步骤出现了两种方法,方法1虽然比较复杂但可以培养学生计算的毅力与钻研精神以及整体的思想;方法2学生可以类比椭圆中移项平方后处理。比较方法1与方法2学生对有2个根号的化简会有更加深刻的认识。
得出焦点在x轴上双曲线的标准方程后让学生类比椭圆的标准方程得出焦点在y轴上的双曲线的标准方程,同时让学生总结a,b,c之间的关系以及与椭圆中的区别。最后通过具体例题让学生辨别如何根据双曲线的标准方程判断焦点在哪个轴上。
在课堂小结中分别从定义、图象、方程、焦点、a,b,c之间的关系对椭圆与双曲线进行区别与联系,同时也是对整个课程回顾,让学生感受到运用类比思想与数形结合思想解决数学问题的重要性。
本节课我需要改进的有以下几点:一是自身专业素养有待提高特别是画图这一块需要注意椭圆的平滑程度;二是对双曲线的定义讲解还不够深入,需要进一步去挖掘定义的来龙去脉;三是课堂板书有待进一步改善;四是解决数学问题题时更重要是暴露解决问题的思维过程,而不是注重解决题结果的分析。
.
/span>