直线和圆的综合问题(一)


教学目标:
1、能熟练运用直线与圆的有关知识解决直线与圆中的最值问题;
2、能熟练运用直线与圆和其他数学知识解决综合问题,有利于培养学生分析问题和解决问题的能力;
3、体会数形结合思想,感受解析几何之美.
教学重点:代数法和几何法在直线与圆中的最值问题的应用
教学难点:运用直线与圆和其他数学知识解决圆的综合问题
一、课前热身
1、圆
![]()
![]()
2、已知
![]()
![]()
![]()
![]()
![]()
![]()
3、若圆
![]()
![]()
![]()
![]()
4、已知圆
![]()
![]()
![]()
![]()
![]()
![]()
二、例题引导
例1、在平面直角坐标系
![]()
![]()
![]()
![]()
![]()
变式1:在平面直角坐标系
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
变式2:在等腰三角形
![]()
![]()
![]()
![]()
例2、直线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
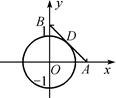
变式:如图,设圆
![]()
![]()
![]()
![]()
![]()
![]()
![]()
三、课堂小结
四、反馈练习
1、若点
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2、当直线
![]()
![]()
![]()
![]()
![]()
3、在平面直角坐标系
![]()
![]()
![]()
![]()
![]()
4、设
![]()
![]()
![]()
![]()
![]()
5、已知⊙
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1) 求实数
![]()
(2) 求线段
![]()
(3) 若以
![]()
![]()
![]()
![]()
直线和圆的综合问题(一)教学反思
当下课铃声响起的时候,我问自己:这节课我上得成功吗?在我的这节数学课中,学生们学到了什么?掌握的得怎么样?还有什么没有掌握?下堂课要给学生强调哪些知识?借用某位大家说的话:思之则活,思活则深,思深则透,思透则新,思新则进。反思自己的教学行为,总结教学的得失与成败,对整个教学过程进行回顾、分析和审视,才能形成自我反思的意识和自我监控的能力,才能不断丰富自我素养,提升自我发展能力。下面我就对这节课在以下几个方面作了一下反思。
一、反思教学行为是否达到了教学目标
这节课总的来说教学目标还是达到了。我利用多媒体投影学生做的题目,以学生为主题,引导学生从几何角度和代数角度两方面体会直线和圆的综合问题处理方式。调动学生积极主动参与数学活动.为深刻理解直线和圆的综合问题的解题思路做好铺垫。解决圆的问题实质上就是找点、线和圆的位置关系转化为圆半径和点、线与圆心的距离的数量关系,并得到解决直线和圆的综合问题的突破口。
二、反思教学过程是否符合学生的认知规律
教学是引导学生在情境中去经历、去体验、去感悟、去创造。这节课根据教学内容编排的例题和练习题,还是比较符合学生的认知规律的,有些练习题设有一些小的陷阱,为的是加深学生对概念的理解,设计的例题能够由易到难,把新的知识转化到旧的、我们熟悉的知识来解,在教学过程中,我始终留意学生在课堂上的一举一动,学生精力集中、反映积极、动作迅速、心情愉快,主动参与,说明学生学有所得。还有检查学生做课堂练习的时候,多数同学能在规定的时间里正确完成规定的题目,说明教学目标基本达到,这节课我充分地发挥学生的个性特长,让每一个学生都有施展才能的机会,让基础好的学生“吃得饱”、跑得快,让中等生“吃得好”、跑得动,让学困生“吃得了”、不掉队。就是尊重学生的个性差异,尽可能地创设条件发展学生的思维能力,培养学生的思维品质,促进全体学生的发展。
四、反思教学过程是否有意识地渗透数学思想方法
这节课用到的数学思想方法还是比较多的,通过直线和圆的位置关系的探究,由轨迹问题,向学生渗透分类、数形结合的思想,培养学生 观察、分析和概括的能力; 使学生从运动的观点来观察直线和圆关系,从多个角度对所学知识加以运用,在教学中,以“形”归纳“数”, 以“数”判断“形”,在教师的组织下,以学生为主体,活动式教学,最后归纳出解决直线与圆的综合问题的几种方法。但是这节课也有有些遗憾的地方,如果提问的方向再明确一些,有针对性一些,也许会使得整堂课显得更紧凑,线索更明朗。
在上这节课前多次向数学组的其他老师请教,多次磨课,非常感谢他们,同时也非常感谢我师父给了我很受用的建议。在上完本节课后,我又积极的向老教师请教,先后向听评本节课的老教师请教,在跟他们交流后发现了自己的不足,操海涛老师指出,本节课的一些措辞要在斟酌一下可能会更好。二中的徐远峰老师指出,本节课已经体现出了学生的主题地位,先学后教,学生互评等措施,给予了肯定,同时也提出了一些建议,在教学环节的时候要注意细节,教师的每句引导的话,每个练习的时间的灵活掌控,对学生的每句评价都要三思而行,还有些小的地方需要改进。
总之课是上完了,我们应该每上完一节课都要很好地进行反思,因为在数学教学中,反思是发现问题的源泉,是优化教学设计、提高教学质量的好方法,是促进认识升华的可靠途径。我国古代的先哲孔子曾经说过“学而不思则罔,思而不学则殆。”国外的学者也对反思的重要性作过阐述。如荷兰数学教育家弗赖登塔尔曾说:反思是重要的数学活动,它是数学活动的核心和动力。美国的波斯纳指出教师的成长=经验+反思。可以说,反思可以使存在的问题得到整改,发现的问题及时探究,积累的经验升华为理论。反思还能提高数学意识,优化思维品质。所以我们要重视反思,只要我们善于观察、善于思考,就一定能逐步提高自身的教学水平,教学质量也一定能够提高。
/span>