3.3 幂函数
常州市第三中学 王逸楠

教材分析:
本节课选自新课程苏教版必修1第3章第3节,幂函数是继指数函数和对数函数后研究的又一基本函数.通过本节课的学习,学生将建立幂函数这一函数模型,并能用系统的眼光看待
![]()
学情分析:
学生通过对指数函数和对数函数的学习,已经初步掌握了如何去研究一类函数的方法,即由几个特殊的函数的图象,归纳出此类函数的一般的性质这一方法,为学习本节课打下了基础.
设计思想:
由于幂函数的性质随幂指数的轻微改变会出现较大的变化,因此要学生在一节课中象指数函数和对数函数那样完全掌握这类函数的性质是比较困难的,因此本人采用了从特殊到一般的方法,重点研究了几个常见的幂函数的图象和性质,从而感受幂函数随幂指数改变的性质变化情况,初步掌握如何去研究一类函数的方法.
教学目标:
1. 知识目标:
(1)了解幂函数的概念;
(2)会画简单幂函数的图象,并能根据图象得出这些函数的性质;
(3)了解幂函数随幂指数改变的性质变化情况.
2. 能力目标:
在探究幂函数性质的活动中,培养学生观察和归纳能力,培养学生数形结合的意识和思想.
3. 情感目标:
通过师生、生生彼此之间的讨论、互动,培养学生合作、交流、探究的意识品质,同时让学生在探索、解决问题过程中,获得学习的成就感.
教学重点:
常见的幂函数的图象和性质.
教学难点:
幂函数图象的画法和性质的总结.
教学用具:
多媒体平台,几何画板课件.
教学过程:
一、幂函数的概念
1.情景引入
(1)某人购买了每千克1元的蔬菜x千克,应付y元,这里x与y的关系是什么?
(2)正方形的边长为x,则它的面积y是多少?
(3)如果正方体的棱长为x,那么它的体积y是多少?
(4)如果正方形场地的面积为x,那么它的边长y是多少?
(5)某人在xs内骑车匀速行进了1km,那么他的速度y(km/s)是多少?
思考:这些函数有什么共同点?他们是指数函数吗?
2. 概念生成
一般地,我们把形如
![]()
![]()
练习:判断下列函数是幂函数的有_______
①
![]()
![]()
![]()
![]()
提问: ③为什么不是呢?指数函数和幂函数有什么区别?
二、幂函数的图像和性质
1、研究方法
①数形结合——画图;
②特殊到一般再到特殊
2、研究过程
①分别画出
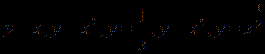
②填写下面表格
|
幂函数 |
|
|
|
|
|
|
|
定义域 |
|
|
|
|
|
|
|
值域 |
|
|
|
|
|
|
|
单调性 |
在
|
在
调递增,在
|
在
|
在
|
在
|
|
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
非奇非偶 |
奇函数 |
|
|
定点 |
(0,0);(1,1) |
过(1,1) |
||||
③根据表格总结幂函数的性质
(1)定点:a>0时,图象过(0,0)和(1,1)两个定点;
a≤0时,图象过只过定点(1,1).
(2)单调性:a>0时,在区间[0,+¥)上是单调递增;
a<0时,在区间(0,+¥)上是单调递减.
(3) 图像(第一象限): a>1,呈抛物线型,下凸递增
0<a<1, 呈抛物线型 ,上凸递增
a<0 ,呈双曲线型, 递减
④由一般再到特殊:画出
![]()
3、结论应用
例1:函数
![]()
![]()
![]()
![]()
例2:比较下列各组数的大小:
(1)
![]()
![]()
例3:已知幂函数
![]()
![]()
![]()
三、课堂小结
1.概念:
形如
![]()
![]()
2.常见幂函数的性质:
|
|
|
|
|
|
|
|
定义域 |
|
|
|
|
|
|
值域 |
|
|
|
|
|
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
非奇非偶 |
奇函数 |
|
共同 特征 |
定点:(0,0);(1,1) |
在
|
|||
3.研究结论
4.数学思想方法:
(1)归纳推理:特殊到一般;
(2)类比推理:类比指数函数结构,知道幂函数是什么,类比指数函数研究方法,知道研究什么,怎么办;
(3)数形结合思想:以形助数,直观明了,依数导形,精确入微.
幂函数的教学反思
我用五个具体的生活实例激活学生的求知欲望,明确将要研究的问题。
通过对指数n的选取,让学生在亲身体验和实践中,形成对图象的认知。在改变学生学习方式的同时,我有了看学生“做数学”的机会。我适时地将几个函数的解析式写在黑板上,引发学生做出判断,这对于每一个学生而言,不仅是参与,更是对幂函数解析式特征的意义建构。我将学生的画图结果通过投影仪展示出来,为后面学生观察归纳幂函数的性质提供素材。然后学生观察图像,总结幂函数的一般性质。
在这节课中,我对于5个常见的幂函数的性质把握不够到位,错把重点放在了幂函数的一般性质上。另外,学生做的图没有很好的利用起来。这些都需要改进。
an>