《幂函数》教学设计

【教学目标】

1. 知识与技能 ：

（1）理解幂函数的概念，会画出幂函数

，

，

，

，

的图象，根据上述幂函数的图象，了解幂函数的变化情况与性质； 

（2）了解几个常见的幂函数的性质，会用它们的单调性比较两个底数不同而指数相同的指数式值的大小.

2. 过程与方法：

（1）类比研究一般函数，指数函数、对数函数的过程与方法，研究幂函数的图象和性质.；

（2）采用从特殊到一般的数学思想，从特殊的幂函数图象及其特征归纳总结到一般幂函数的共有性质；

（3）进一步渗透数形结合与类比的思想方法.

3. 情感、态度、价值观：

在民主和谐的课堂氛围中体验学习的乐趣.

【教学重点、难点】

教学重点：从具体的幂函数中认识一般幂函数的概念和性质 ；

教学难点：从幂函数的图象中概括其性质.

【教学过程设计】

一、问题情境

前几节课刚刚接触了指数函数与对数函数两类模型，在现实生活中往往会结合实际问题来建立函数模型，下面来看几个具体问题：

1.某人购买了每千克1元的蔬菜

千克，那么他需要付的钱数

为多少元？

2.正方形的边长为

，则它的面积

是多少？

3.正方体的棱长为

，则它的体积

是多少？

4.如果正方形场地的面积为

，那么它的边长

是多少？

5.某人在5秒内骑车匀速行进了1

，那么它的速度

（

）是多少？

【思考】上述函数是指数函数吗？它们有何共同特征？

【学生活动】幻灯片展示问题，学生口答并归纳上述函数的共同特征：（1）都是幂的形式；（2）幂的底数是变量，指数是常数.

【教师总结】一般形式：

（

是常数）.

二、概念形成

1、幂函数定义：

一般地，我们把形如

的函数称为幂函数，其中底数

是自变量，指数

是常数.（形式定义）

【概念辨析】

（1）幂函数与指数函数有何区别？

【师生活动】引导学生从函数的解析式入手，进行对比，总结归纳：

（2）幂函数的形式特征是什么？

【师生活动】引导学生类比指数函数、对数函数的形式特征，寻求幂函数的形式特点：

（3）小试牛刀：判断下列函数是幂函数的有                ：

①

；②

；③

；④

；⑤

（

为常数）

【例1】写出下列函数的定义域，并分别指出它们的奇偶性：

（1）

；（2）

；（3）

【设计意图】例1的安排是为之后研究幂函数的图象作铺垫，利用数形结合的数学思想，我们可以通过函数的图象总结归纳函数的性质，反之，函数的性质也可以为作图提供便利，如单调性可以判断函数的变化趋势等等

2、幂函数的图象与性质：

【数学思想】

（1）类比一般函数、指数函数与对数函数的研究过程，明确下一步的学习目标——幂函数的图象与性质；

（2）研究新定义的一类函数的图象采用从特殊到一般的思想方法.

【探究活动】

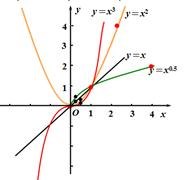
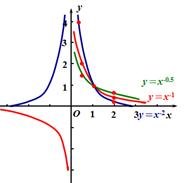
分别在同一坐标系中作出每一组函数的图象：

（1）

，

，

，

；  （2）

，

，

.

【师生活动】学生自己作图，教师巡视引导，寻找学生作图时遇到的困难与遗漏点，然后再借助几何画板或者幻灯片展示作图的过程.

（1） ：描两个点 ， ； （2） ：定义域为 ，偶函数，所以只需在 上取点，如取 ， ， ，作出它在第一象限内的图象，然后利用奇偶性补全另一半； （3） ：定义域为 ，奇函数，所以只需在 上取点，如取 ， ， ，【但在连线的过程中发现学生没有关注与坐标系中已有的曲线进行比较，如当 时， 的图象是夹在 与 之间，还是在 下方，因而在此处我引导学生通过取关键点的作法来确定其变化趋势，如取 ，比较纵坐标的大小来确定其位置】，作出它在第一象限内的图象，然后利用奇偶性补全另一半； （4） ：同上.	（1） ：定义域为 ，奇函数，在 上取点 ， ， ，描点连线作出其在第一象限的图象，再利用奇偶性补全另一半； （2） ：定义域为 ，偶函数，在 上取点 ， ， 【与 相比，取同一横坐标下的点便于确定几个函数的变化趋势，为之后研究幂函数的性质作铺垫】，描点连线作出其在第一象限的图象，再利用奇偶性补全另一半； （3） ：同上述（2）.

【总结】在作幂函数

图象时应注意：（1）定义域；（2）利用奇偶性：先作出

时的图象，再补全

时的图象；（3）通过取关键点判断函数图象的变化趋势.

【问题1】观察上述函数的图象，你有什么发现？请你完成下列表格.

定义域
值域
奇偶性
单调性

【问题2】你能否从中总结出一般幂函数的共有性质？

【学生活动】类比指数函数、对数函数的性质，学生小组讨论幂函数的性质,教师在巡视的过程中进行适当引导.

【数学建构】幂函数的一般性质：

（1）定义域：与

的取值有关

所有的幂函数都在

上有定义，且在第一象限均有图象.

（2）单调性：

幂函数

仅在

上都有定义，因而只研究其在

上的单调性.

当

时，

在

上单调递增；

当

时，

在

上单调递减.

（3）定点：

当

时，

恒过定点

，

；当

时，

恒过定点

.

（4）指数大小对幂函数图象的影响：

当

时，指数大线在下；当

时，指数大线在上.

三、数学应用

【例1】函数

是幂函数，且当

时，

是增函数，求

的解析式.

【设计意图】进一步熟悉幂函数的形式特征以及指数对幂函数单调性的影响.

【例2】比较下列各组数的大小：

（1）

，

；（2）

，

；（3）

，

.

【设计意图】幂函数单调性的简单应用.

四、课堂小结

本节课我们主要学习了幂函数，你有什么收获与困惑？

1、幂函数的定义

2、幂函数的图象与性质

3、思想方法：类比、从特殊到一般、数形结合

《幂函数》教学反思

幂函数作为一类重要的函数模型，是学生在系统学习了指数函数、对数函数之后研究的又一类基本初等函数。学生已经有了学习指数函数和对数函数的图象和性质的学习经历，幂函数概念的引入以及图象和性质的研究便水到渠成。

首先我由生活中的五个实例引入，概念过渡自然，学生易于接受。我引导学生从实例出发，通过几个具体的幂函数，归纳出这类函数的共同特征，引出幂函数的概念，之后，为了强化概念，我采用步步设问、课堂讨论、练习等方式来加深理解。在这个环节上，部分学生出现了两个问题：一是把幂函数和指数函数混为一谈了；二是对幂函数的形式特征归纳不到位。针对这两个问题，我对学生强调了幂函数和指数函数的区别，并通过练习让学生认识幂函数的形式特征。

其次，在教学过程中，我类比研究一般函数、指数函数、对数函数的过程与方法，来研究幂函数的图象和性质。从特殊到一般，在教学中我给了两类具体的幂函数，要求学生亲自动手做图，在巡视的过程中一方面知道部分学生如何作图，一方面观察总结学生在作图中所忽略的关键因素，然后再借助电脑手段，利用幻灯片展示描点作图的过程，并向学生强调了作图需要关注的几个因素：（1）定义域；（2）奇偶性；（3）利用取关键点的方式确定函数的变化趋势。然后利用数形结合的思想引导学生说出图像特征及变化规律，并从而归纳一般幂函数的性质，在此过程中我发现大部分学生课堂上能积极主动参与获得性质的过程，并学会处理未知问题的方法。最后，通过例1（求幂函数的解析式）与例2（比较大小）加深学生对幂函数性质的理解。

本节课的成功之处在于：（1）教学时间上的安排比较合理，30分钟的概念形成过程与10分钟的课堂练习，顺利完成本节课的教学任务；（2）为了调动学生学习的积极性，使学生变被动学习为主动愉快的学习，教学中我引导学生积极参与教学，在对幂函数图象的画法上，我指出学生画法上的不足，如在作y＝x³图象时，我发现学生没有关注图象的变化趋势，如当0<x<1时，图象是夹在y＝x的图象与y＝x²的图象之间，还是在y＝x²图象的下方，学生只是凭感觉随手一画，在此我通过取关键点的方法，并借助电脑，演示作图过程及图像变化的动画过程，从而使学生直接地接受并提高学生的学习兴趣和积极性，很好地突破难点和提高教学效率，从而增大教学的容量和直观性、准确性，为之后判断指数大小对幂函数图象的影响作铺垫。

本节课的不足之处在于：（1）在引导学生作幂函数的图象过程中，我认为更好的处理方式是留有充足的时间安排学生分组作图，然后通过投影部分学生的作图，与学生共同探讨并点评他们作法的优缺点，让学生能更好地接受新知，加深印象，但由于教学时间比较紧凑，在作图的过程中，我只留了3分钟左右让学生自行作图，之后通过自己在巡视中对学生作图不足之处的总结，直接通过幻灯片放映展示了作图的关键因素；（2）在分析作图方法的不足之处时，应充分发挥学生的主体性，让学生自己来分析点评，引导学生积极地观察问题，分析问题，激发学生的求知欲和学习积极性，指导学生积极思维、主动获取知识，养成良好的学习方法。这些不足还有待于我在以后的教学中摸索并改进。

an>