

试卷讲评数形结合问题
教学目标:
1、 知识目标:理解“数形结合”思想在高中解题中的重要应用,并能掌握解决此类问题的基本技能.
2、 能力目标:培养分析、解决问题的能力,体验“数形结合”思想在高中数学中与“方程”,“函数”和“ 平面向量”,“解析几何”等模块的具体应用.
3、 情感目标:(1)在探究过程中,鼓励学生大胆猜测,大胆尝试,培养学生勇于创新、敢于实践的个性品质;(2) 通过对问题的探究,理解事物间普遍联系与辩证统一观点,体验成功的喜悦.
教学重点:理解“数形结合”思想的实质,有效掌握该类问题的基本技能.
教学难点:利用“数形结合”思想,通过“以形助数”,使复杂问题简单化,抽象问题具体化,能够变抽象思维为形象思维.
教学过程:
13.已知函数
![]()
![]()
![]()
则m的取值范围是 .
![]()
变式:
已知函数
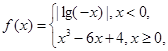
![]()
![]()
![]()
![]()
12.在△
![]()
![]()
![]()
![]()
![]()
11.如图,在平面四边形
![]()
![]()
![]()
![]()
![]()
![]()

变式:
已知
![]()
![]()
![]()
![]()
![]()
![]()
已知
![]()
![]()
![]()
![]()
![]()
![]()
教学反思:
数学家华罗庚曾经说过:“数与形本是相依,怎能分作两边飞,数缺形时少直观,形少数时难入微”,所谓的数形结合就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想。简而言之就是一种数形之间取长补短,优化解题的一种思路。在高中实际解题运用中,数形结合又是一种能力,它没有固定刻板的模式,本节课中通过试卷上的几个中档题,指导学生在独立思考中充分利用自己的思维能力以及数学经验,巧妙地察觉出题目中抽象的数学语言和与之相应的几何图形的联系,从中搭建一条桥梁,灵活转化,简洁,有效地解决题目。本节课从学生熟悉的函数方程知识入手,通过图像,形象直观的运用数形结合的思路解题。然后利用试卷上的平面几何,平面向量两个问题进一步探讨比较代数法与几何法,充分体会数形结合对解决问题的巨大作用。讲评课不能就题论题,针对学生的错题还应多角度、多层面引导学生思考,同时注意知识的拓展深化,帮助学生进一步理解知识、熟练技能、查漏补缺、总结经验、拓宽思路、揭示规律、提高能力。
an>