数形结合解决解析几何问题

一．教学目标

1.能熟练识别、运用数形结合的方法解决一些解析几何问题；

2.在问题解决的过程中领会数形结合思想，并感悟其优越性．

二．教学重难点

运用数形结合的方法解决数学问题的几种常见途径．

三．教学过程

（一）引入：

1、试卷第18题：

 已知圆

，相互垂直的两条直线

、

都过点

.

（1）当

时，若圆心为

的圆和圆

外切且与直线

、

都相切，求圆

的

方程；

（2）当

时，求

、

被圆

所截得弦长之和的最大值，并求此时直线

的方程.

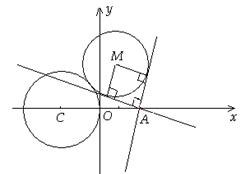
2、试卷第13题：

已知圆M：

，过

轴上的点

存在一直线与圆M相交，交点为A、B，且满足PA=BA，则点P的横坐标

的取值范围为                    ．

 

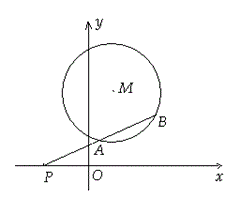
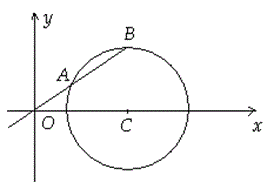
变式：（2016 苏锡常镇一模）

在平面直角坐标系xOy中，已知过原点O的动直线l与圆C：x2＋y2－6x＋5＝0相交于不同的两点A，B，若点A恰为线段OB的中点，则圆心C到直线l的距离为________．

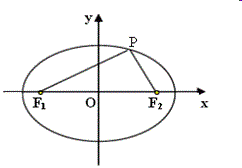
4、试卷第9题：

若A、B与 F₁、F₂分别为椭圆C：

的两长轴端点与两焦点，椭圆C上的点P使得∠F₁PF₂= eq \f(π,2)，则tan∠APB=           ．

（二）总结反思

数形结合是把数（或数量）关系与图形对应起来，借助图形来研究数量关系或者利用数量关系来研究图形的性质，是一种重要的数学思想方法。它可以使抽象的问题具体化，复杂的问题简单化。

要根据问题的具体情况，注意改变观察和理解问题的角度，揭示问题的本质联系，用“数”的准确澄清“形”的模糊，用“形”的直观启迪“数”的计算，从而使问题得到解决。

因为解析几何本身就是数形结合的典范，而且在研究几何图形的性质时，也充分体现“形”的直观性和“数”的严谨性。直线和圆是学生非常熟悉的两种图形，学生已经知道如何从“形”的角度分析直线和圆的位置关系，在数学学习和解题过程中，要善于运用数形结合的方法来寻求解题途径，制定解题方案，养成数形结合的习惯，解题先想图，以图助解题。

用好数形结合的方法，能起到事半功倍的效果。通过数形结合思想方法，培养学生能提出问题和解决问题的思维方式，学会反思，从而提高学生综合解题的能力。

an>