同课异构,同放异彩

9月8日,2016学年高中数学同课异构课堂展示活动在常州市第一中学举行。侯卫婷老师代表我校参与了本次活动。同课异构是指选用同一教学内容,根据学生实际、现有的教学条件和教师自身的特点,进行不同的教学设计。它要求教师精心研究教材,潜心钻研教法和学法,以便各显风采,各具特色,为集体研讨提供很好的研究平台。它是教师提高教学水平和教学能力,总结教学经验的一条有效途径。本次展示活动上课的两位教师都是有十余年教学经验的成熟教师,但在对内容的理解,教法的选择,重点的渗透上,仍旧体现出了不同的认识,各有风采。侯老师把重点放在概念的构建,公理化体系的认知上,而丁老师则强化了模式的选择和操作的指向性。在课后的教学研讨中,教研员孙福明老师评价道:同课异构是为了教学高效,教学高效是为了学生受益。教师关注的不仅仅是学生的现在,更是把学生的未来、学生的健康成长和发展作为了自己的使命,高效教学的最终受益者就是学生了。 同课异构的教研方式,可以引发参与者智慧的碰撞,可以长善救失,取长补短,明显提高教育教学效果,同时也为教师们提供了一个面对面交流互动的平台。在这个平台中,老师们共同探讨教学中的热点,难点问题,探讨教学的艺术,交流彼此的经验,共享成功的喜悦。 (侯卫婷)
直线与平面平行判定定理
内容分析:本节内容是苏教版必修二1.2.3的内容。此前,学生已经认识了空间几何体,研究了点、线、面之间的关系,对于立体几何的研究对象和思维方式都有了一定的学习基础。从直观感知的角度,线面平行是空间中一种最基本的位置关系,在几何体中大量存在,学生有良好的认知基础;从逻辑推理的角度,平行的证明并不困难,但学生在证明的严谨性和思维的严密性上会有缺失,对于公理化体系的认识尚不深刻,正是教师发挥主导作用,帮助学生进一步学习公理化体系,培养理性思维的要点所在。
学情分析:授课对象为四星级高中高二理科班的学生,学生的基础很好,思维很活跃,配合度较高。有利于通过交流对话,思维互动形成较好的课堂效果。
教学过程:
引入:观察三棱柱
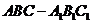
1.共有多少条棱?
2.这些棱所在的直线与面
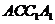
3.空间中的直线和平面的位置关系,除了这三种,还有别的可能吗?
4.让我们来画一画三种位置关系。
5.让我们用符号语言来描述这些关系。
新课
1.研究新定理。
刚才我们定义了空间中的线面平行。从直观感知上,大家认为直线
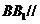
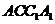
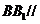
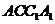
事实上,由于直线和平面都是无限的,而我们通过作图只能画出其中的一部分,所以很难说明直线和平面是没有交点的。那么,我们可以换个思路。观察三棱柱
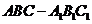
结构性提问:这个条件有用吗?怎么用(有这些条件足够了吗?)
凑足三个条件后:这里面有没有多余条件?
这些条件能帮我们准确说明线面平行了吗?
让我们把这个研究的过程形成一个结论。你能分别用图形,符号,文字来描述我们刚才得到的结论吗?
我们把它称之为:直线与平面平行的判定定理
2.形成新定理。
为什么要研究判定定理?
它的作用是什么?
利用判定定理来解决线面平行问题,首先要去寻找的是?
3.定位新定理。
判定定理正确吗?为什么?
在公理化体系中,有那个现有公理直接支持判定定理?没有。
所以,判定定理也需要证明。如何证明?
4.应用新定理。
例题1:在正方体
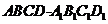
(1)且与直线
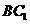
(2)且与直线
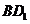
5.课堂小结
/span>